Probing LLM Numeracy

Modeling Low-Dimensional Internal Representations of Numbers of Large Language Models

đź“„ PDF

Do AI models think about numbers like children or adults?

While Large Language Models like GPT-4 excel at many tasks, they surprisingly struggle with basic arithmetic—achieving only 58% accuracy on elementary math problems. This project investigates why by examining how these models internally represent numbers.

The Core Question

Using a cognitive science approach borrowed from child development research, I asked: How does GPT-4 mentally organize numbers? Does it think like an adult with sophisticated mathematical understanding, or more like a child just learning to count?

Methodology

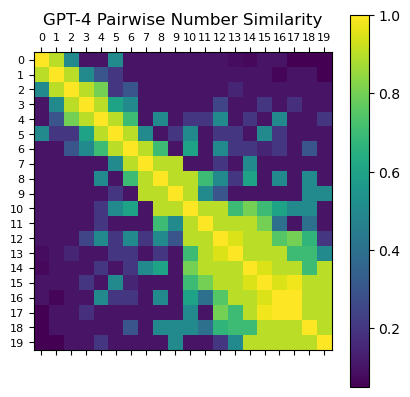
I applied multi-dimensional scaling (MDS) to pairwise similarity judgments, asking GPT-4 to rate how similar pairs of numbers (0-19) are to each other. This same technique has been used for decades to understand how children develop numerical reasoning.

Left: GPT-4's similarity judgments show strong diagonal structure (numbers close in magnitude are rated as similar). Right: Adult humans show more complex patterns reflecting mathematical properties beyond magnitude.

Key Findings

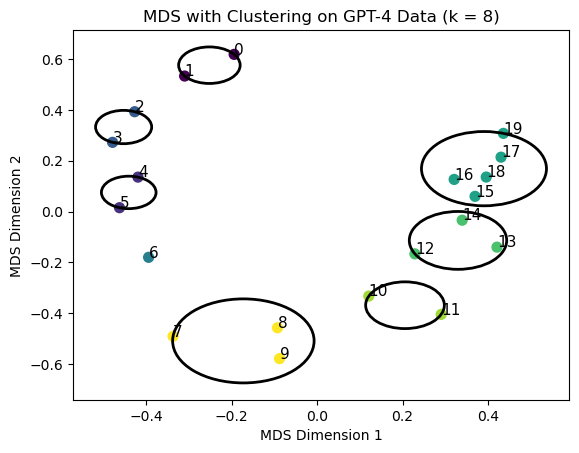
GPT-4 thinks about numbers like a kindergartner. The spatial representation extracted from GPT-4’s similarity judgments arranges numbers in a simple curved line by magnitude—identical to patterns found in young children who haven’t yet learned basic mathematics.

MDS spatial representations reveal GPT-4's sequential number line (left) versus adults' complex web of relationships (right).

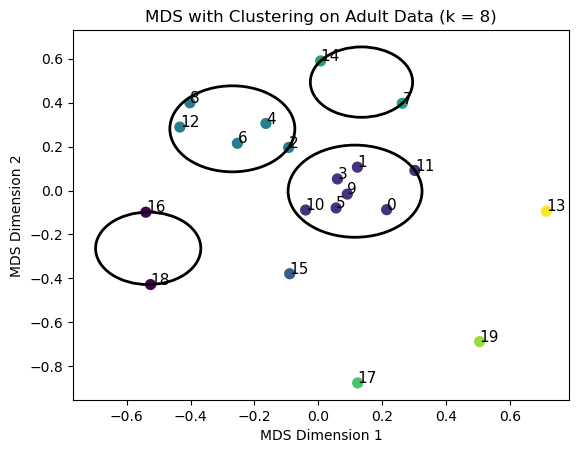
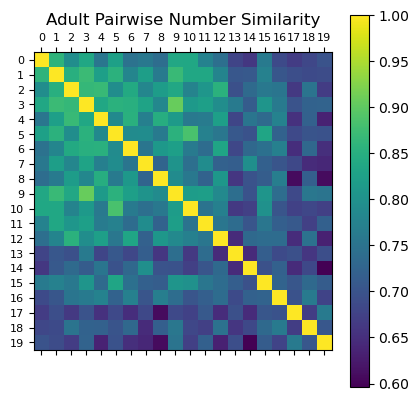
In contrast, adults organize numbers using sophisticated mathematical properties:

  • Odd vs. even numbers
  • Prime numbers
  • Powers of two
  • Divisibility relationships
  • Composite numbers

The correlation between GPT-4 and adult representations? Just r = 0.018—essentially zero.

What This Means

Dendrograms showing how GPT-4 (left) groups numbers strictly by consecutive ranges, while adults (right) use mathematical properties like primes, composites, and divisibility.

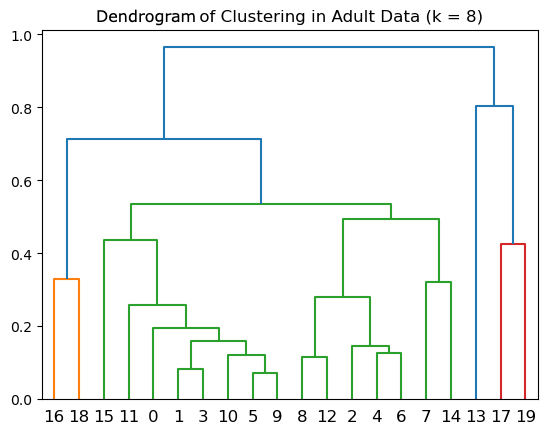
This child-like representation suggests that GPT-4 hasn’t truly learned fundamental mathematical concepts—it’s operating at the level of basic counting rather than mathematical reasoning. This explains why it struggles with arithmetic: it lacks the sophisticated internal number sense that humans develop through mathematical education.

Implications

Simply training on more arithmetic data may not be enough. Like children need to learn concepts like “evenness,” “primeness,” and “divisibility” to reason mathematically, LLMs may need explicit inductive biases or structured training to develop adult-level numerical understanding.

This work provides a benchmark for evaluating future LLMs: as models improve, their internal representations should shift from child-like magnitude-based organization toward adult-like mathematical abstraction.

Research conducted at Princeton University
Advised by Tom Griffiths | Special thanks to Raja Marjieh and Ilia Sucholutsky